회귀; regression, 되돌아옴.
되돌아올 시간입니다.
안녕하세요, 오늘은 컴퓨터비전 분야에서의 Linear Regression, 선형 회귀 분석에 대해 알아보겠습니다. 본격적인 이론에 들어가기에 앞서 회귀에 대한 흥미로운 얘기를 좀 해보겠습니다.

유전이라는 자명한 법칙에 따르면, 평균에 비해 확실히 키가 큰 아버지가 아들을 낳으면 그 아들은 키가 클 확률이 높습니다. 그러나, 그 아버지보다는 작을 확률이 높습니다. 반대로 키가 작은 아버지가 아들을 낳으면 아들도 작겠지만, 그 아버지보다는 클 확률이 높습니다. 만약 전자에서 아들이 아버지보다 더 커지거나, 후자에서 더 작아질 확률이 높다면 우리의 키는 각각 ∞ 와 0으로 수렴할 것입니다. 그렇지 않기에, 키와 같은 특성은 세대를 거듭할수록 평균에 가까워집니다.
위의 이야기는 19세기 영국의 학자 프랜시스 골턴이 주장한 '평균으로의 회귀, Regression toward the mean' 의 예시입니다. 극단적이거나 이례적인 결과는 결국 평균 방향으로 되돌아오는, 회귀하는 경향을 가진다는 것이죠. 골턴은 이 현상을 증명하기 위해 회귀분석을 만들었습니다. 그리고 이 회귀분석이 유명해짐에 따라, 오늘날의 '회귀; 평균으로 돌아간다'는 의미는 거의 사라졌습니다.
선형 회귀(Linear Regression)는 하나 이상의 독립변수 X와 종속변수 Y의 선형 상관 관계를 모델링하는 회귀분석 기법입니다. 앞선 이야기에서 독립변수 X는 아버지의 키, 종속변수 Y는 그 아들의 키가 될 것입니다. 여기서 유전적 요소인 아버지의 키를 유일한 독립변수 X로 놓았는데, 이 처럼 한 개의 독립변수만 있다면 이는 단순 선형 회귀라 부릅니다.
아들의 키에 영향을 끼치는 건 사실 아버지의 키를 제외하고도 많을 것입니다. 성장기에 밥은 잘 먹고 다녔는가, 일찍 잘 잤는가, 농구를 하였는가, 우유를 많이 마셨는가 등등이 있겠죠. 이런 변수들을 모두 독립변수에 포함시키는 경우, 독립 변수가 둘 이상인 다중 선형 회귀가 됩니다.
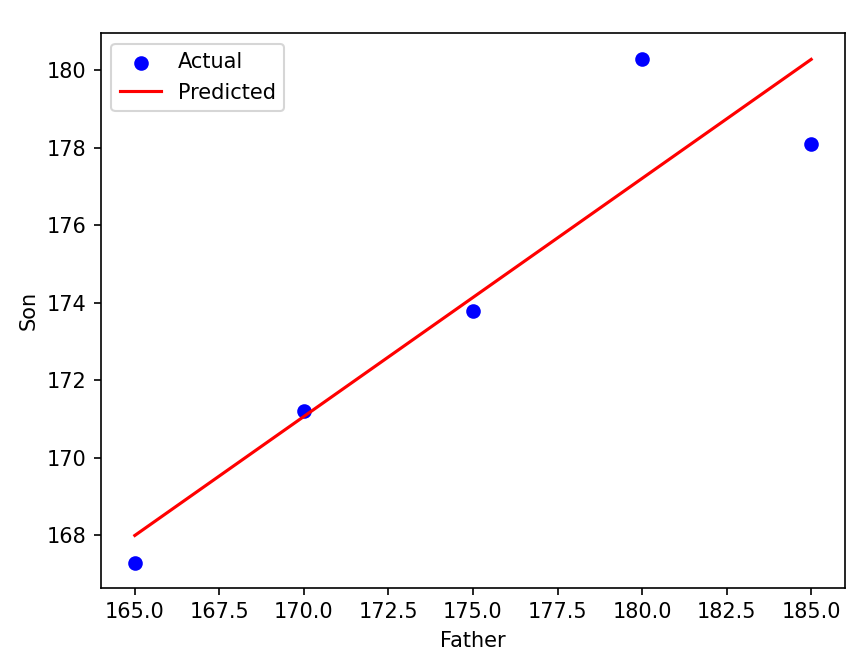
위의 그래프는 x축을 아버지의 키로, y축을 아들의 키로 추정한 단순 선형 회귀 모델입니다. 수학/통계학 등에서 사용되는 '선형'이란, 쉽게 생각하면 직선입니다. 선형 모델은 1차함수로 나타내어지는 모델이라고 생각할 수 있습니다. 2차함수, 로그함수, 삼각함수 등은 비선형으로 분류되고, 시너지 혹은 피드백 등의 부가 현상으로 비선형이 되는 경우가 많습니다.
위의 이미지를 결과로 갖는 파이썬 코드 밑에 첨부합니다. 직접 값을 조정하며 눈으로 확인해보셔도 좋겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 샘플 데이터 생성
X = np.array([[165], [170], [175], [180], [185]])
Y = np.array([167.3, 171.2, 173.8, 180.3, 178.1])
# 선형 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X, Y)
# 예측 값 계산
Y_pred = model.predict(X)
# 결과 시각화
plt.scatter(X, Y, color='blue', label='Actual')
plt.plot(X, Y_pred, color='red', label='Predicted')
plt.xlabel('Father')
plt.ylabel('Son')
plt.legend()
plt.show()
아버지의 키를 x, 아들의 실제 키를 y, 아들의 예측 키를 y'으로 놓게 되면 y' = ax + b 라는 간단한 선형 모델이 탄생합니다. 여기서 a는 회귀 계수(가중치)이며, b는 절편으로 데이터가 얼마나 bias 되었는가를 의미합니다. 오차는 | y - y' | 이 되겠죠?
만약 충분한 데이터셋과 그를 잘 반영한 선형 모델이 존재한다면, 새로 들어오는 아버지의 키만 알아도 그 아들의 키를 그럴듯하게 예측해볼 수 있겠죠. 그럼 여기서 a와 b의 값을 어떻게 설정해야할까? 지금부터 알아보겠습니다.
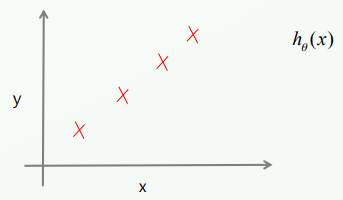
붉은색 X로 표시된 점은 각각의 데이터(실제 값)이고 이 데이터들을 토대로 hθ(x) 라는 선형 모델(일차함수) 2개를 만들어보겠습니다.
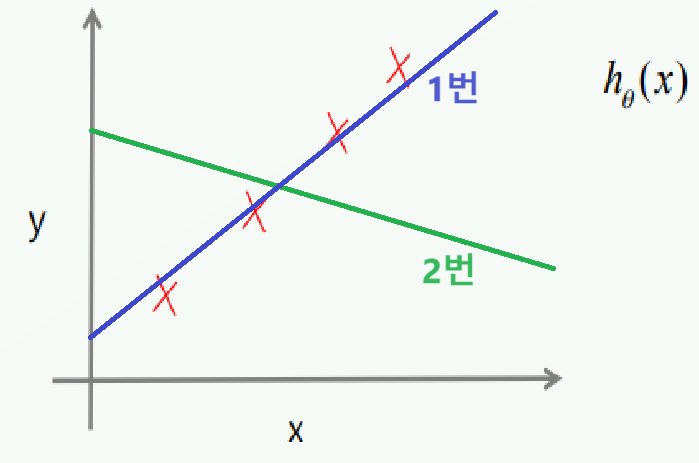
1번 모델과 2번 모델 중 어느 것이 데이터의 경향성을 잘 반영한 걸까요? 당연하게도 답은 1번 모델입니다. 2번 모델은 데이터와 선형 모델의 차이가 너무 커서 제대로 된 선형회귀분석 모델이라고 볼 수 없으며, 1번 모델은 그 차이가 최소이기에 최선의 선형회귀분석 모델이라고 할 수 있습니다.
이처럼 선형 모델을 만들 때에는 내가 만드는 선형 모델의 예측값이 실제 데이터 값과 비슷해야 합니다. 비슷하다는 건 내가 예측한 값과 실제 데이터 값의 오차가 최소화 된다는 것이며, 각 데이터에 대한 오차의 합이 최소가 되었을 때가 최선의 상황이겠죠. 이러한 오차의 합을 비용 함수(혹은 손실 함수)로 나타내고, 이를 최소화 하는 것이 비용 함수 최적화입니다.
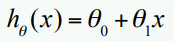
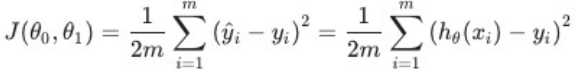
여기서 J는 비용 함수(cost function), θ0은 bias, θ1은 회귀 계수, m은 데이터의 개수, h(x)는 예측 값, y는 실제 값을 의미합니다. 이를 최소화하는 대표적인 방법으로 경사하강법(Gradient descent)에 대해 알아보겠습니다.

이미 사진을 보시면 아시겠지만, 경사하강법에서는 초기 (θ0, θ1) 값을 (0,0) 으로 줍니다. 데이터셋이 (0,0)으로 이루어진 게 아니라면 당연하게 비용함수 J의 값은 크게 나올 것입니다. 이를 줄이기 위해 편미분을 이용합니다. 비용함수 J는 θ1이라는 회귀 계수에 대한 2차함수이기에, 이를 θ1에 대하여 편미분한 값에 학습률 a(learning rate)를 곱하여 θ1 값을 재조정해주는 것입니다.
쉽게 풀어서 설명하자면, 비용함수 J에서 회귀계수 θ1에 대한 기울기를 계산하여 그 반대방향만큼 θ1를 업데이트 해주어 비용함수를 점진적으로 감소시키는 방법입니다. 학습률을 조정하면서 말이죠.

위의 2차 함수는 θ1에 대한 비용함수 J를 나타냅니다. 맨 위의 수식처럼 θ1를 조정할 때에 만약 학습률에 해당하는 a의 값이 너무 작다면 최적의 회귀 계수를 향해 θ1 값이 천천히 조정되기에 최적의 계수를 찾는 수렴은 보장되지만, 속도가 느릴 수 있습니다. 반대로 a의 값이 너무 크다면, 최적의 θ1을 찾기 위해 연산량이 줄어들 수 있지만 최적의 θ1을 향해 수렴하지 못하고 진동할 수 있습니다. 이를 θ0까지 고려한 3차원 좌표공간에서 나타내면 다음과 같습니다.

위 사진을 보면 알겠지만, 편미분 값에 따라 하강을 하기에 자칫 잘못된 방향으로 하강을 하게 되면 local optima에 빠질 수 있는 가능성이 존재합니다. 그래서 이를 방지하기 위해 볼록함수, Convex function을 사용하기도 합니다.

위의 예시가 비용함수 J를 Convex function을 3차원 좌표공간에 나타낸 사진입니다. 시작점에 관계없이 언제나 유일해인 global optima를 찾아갈 수 있습니다. 밑에서 경사하강법을 이용해 최적의 해를 찾아보는 코드와 결과 살펴보겠습니다.
import numpy as np
import matplotlib.pyplot as plt
# 데이터 생성
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 파라미터 초기화
theta = np.random.randn(2, 1)
# 학습률 설정
learning_rate = 0.1
iterations = 1000
# X 데이터에 바이어스 항 추가
X_b = np.c_[np.ones((100, 1)), X]
# 경사하강법 함수
def gradient_descent(X, y, theta, learning_rate, iterations):
m = len(X)
for iteration in range(iterations):
gradients = 2/m * X.T.dot(X.dot(theta) - y)
theta -= learning_rate * gradients
return theta
# 경사하강법 실행
theta = gradient_descent(X_b, y, theta, learning_rate, iterations)
# 예측 값 계산
X_new = np.array([[0], [2]])
X_new_b = np.c_[np.ones((2, 1)), X_new]
y_predict = X_new_b.dot(theta)
# 결과 시각화
plt.plot(X_new, y_predict, color='red', label='Prediction')
plt.scatter(X, y, color='blue', label='Actual data')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()
print("Theta values:", theta)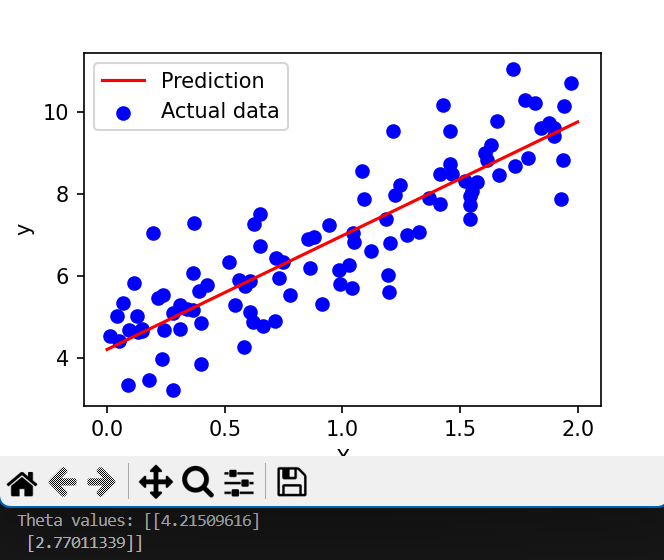
지금까지 선형회귀분석, Linear Regression에 대해 알아보았습니다.
선형회귀분석은 이미지 상에서의 객체 및 특징점 검출, 복원, 추적 등에 널리 쓰이는 기술입니다. 또한 딥러닝과 같은 복잡한 모델에서의 초기 단계 예측, 추후에 배울 과적합과 과소적합 등의 초석이 되기에 알아두면 좋을 것 같습니다.
오늘 하루도 힘든 공부 하느라 고생 많으셨습니다.
'컴퓨터비전 (CV)' 카테고리의 다른 글
| [컴퓨터비전] (4) Image Segmentation, 이미지 분할 (0) | 2024.07.12 |
|---|---|
| [컴퓨터비전] (3) Shape에 대하여 (0) | 2024.06.14 |
| [컴퓨터비전] (2) Texture 에 대하여 (2) | 2024.06.13 |
| [컴퓨터비전] (1) Color, Edge에 대하여 (0) | 2024.03.31 |



