안녕하세요, 개강 무렵 시작한 첫 글이지만 여러 핑계로 종강 무렵에 후속편이 나오게 됐습니다.
게으름을 반성하며 잡설은 줄이고 바로 공부 시작하겠습니다.
지난 글에서 Image feature 중에서 low-level에 해당하는 Color와 Edge에 대해서 알아보았습니다.
오늘은 mid-level에 해당하는 Texture에 대해 알아보겠습니다.

high-level에는 Object, Scene 등이 존재하겠네요.
사담이지만, 저는 수업 시간에 Texture가 mid-level feature 라고 배웠으나 GPT님은 low-level로 분류했습니다.
저는 저희 교수님을 믿기에 당당히 mid-level로 적어놓았으나, 확실히 아시는 분이 계시다면 댓글 좀 남겨주십쇼.
[1] Texture : 이미지에서 반복되는 패턴이나 구조
Texture에 대해 간단히 말해보자면, Image 상에서 반복되는 패턴입니다.
예시로 체크셔츠 사진 속 옷의 체크무늬, 잔디밭 사진 속 잔디들의 배열, 나무 껍질 사진의 껍질 표면 등이 되겠습니다.
이러한 Texture는 Image 공간 안에서 반복되기에 단위는 region입니다.
Texture를 분석할 때 참고할 수 있는 3요소가 있는데, 밑의 3가지라고 수업시간에 배웠습니다.
- 1. 패턴이 Regular하게 or Random하게 반복되는가?
- 2. 패턴의 Size가 큰가 or 작은가?
- 3. 패턴의 방향성?
1번의 예시로 regular한 패턴은 체크셔츠의 체크무늬일 것이고, random한 패턴은 바위산 사진 속 무작위하게 나열된 바위들일 것입니다.
바위들을 찍은 image와 모래들을 찍은 image를 비교해 size를 크다(coarse) / 작다(dense)로 나눌 수 있을 것이고,
하늘의 구름을 찍은 사진은 대부분 가로 방향성을 띄고, 숲의 나무들을 찍은 사진은 세로 방향성을 띌 것입니다.

예시로 위의 Image 속 공대생의 상징... 체크셔츠의 경우 패턴은 Regular 하며, 사이즈는 상대적이지만 coarse한 것으로 보입니다. 그리고 방향성 같은 경우는 가로/세로 양방향의 十 방향성을 가지겠습니다!
이러한 texture를 분석할 때는 3가지 방법이 사용되는데 구조적 방법과 통계적 방법, 모델링이 있습니다.
이 중에서 통계적 방법은 variance, gradient, histogram 등을 사용하여 정량적으로 이미지를 분석하는 기법인데
color를 기반으로 하는 기법엔 LBP, GLCM 등이 있으며 edge 기반 분석 방법에는 Law's energy 가 있습니다.
이 대표적인 텍스쳐 분석 기법의 자세한 사항은 추후에 다루어보도록 하겠습니다.
다음은 없을 것 같아 지금 다루겠습니다.
[1] - 1. LBP (Local Binary Pattern)
남들과의 비교는 좋지 않지만, 항상 좋은 것만 하고 살 순 없습니다.
3x3 Image 에서 가운데 위치한 픽셀이 '나'라고 해봅시다. LBP는 나의 주변 픽셀 8개와 나의 값을 비교합니다.
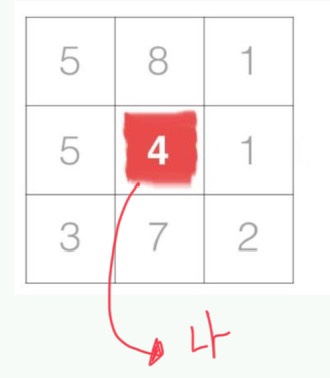
나(4)와 주변 픽셀을 하나씩 비교합니다. 나보다 해당 픽셀의 값이 크면 그 픽셀에 1을 쓰고, 같거나 작으면 0을 씁니다.
그럼 밑에 있는 그림과 같은 새로운 3x3 LBP matrix가 나오게 됩니다.
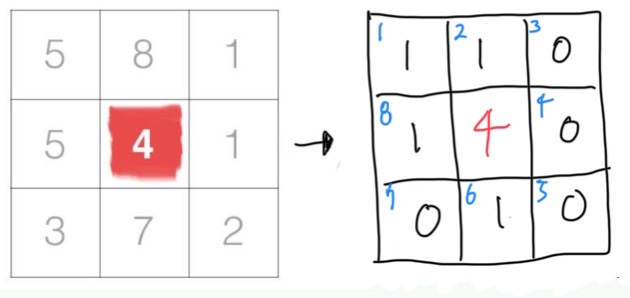
우측의 3x3 LBP matrix의 각 픽셀의 좌상단에 위치한 파란색 숫자는 순서를 의미합니다. 순서는 바로 뒤에 나올 비트 계산에 쓰이는데, 순서를 어떻게 설정하는지 정해진 국룰은 없고 그냥 개발자 맘이라고 합니다. (와우~)
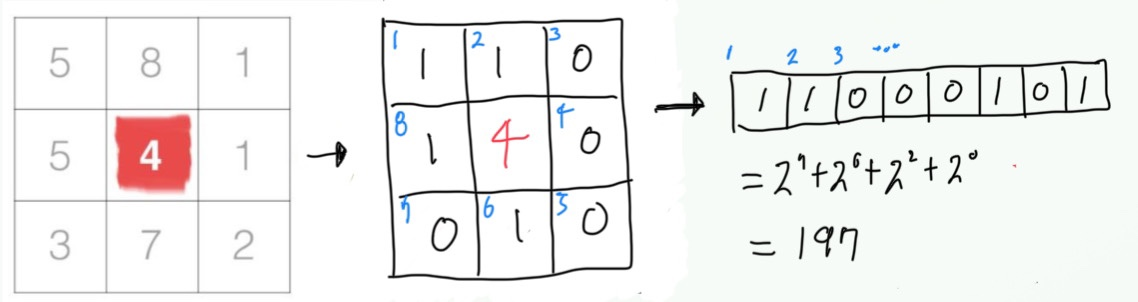
그렇게 완성된 LBP Matrix를 순서에 맞추어 8-bit 배열로 만들어 이진법으로 계산하게 되면 197이라는 숫자가 나오고, 이 값이 원래 '나' 였던 빨간색으로 표시된 픽셀의 값이 됩니다. 이 작업을 모든 픽셀에 해주어 나오게 되는 것이 LBP matrix일 것이고, LBP matrix 값이 크다는 것은 주변보다 어둡다는 뜻으로 해석할 수 있겠습니다.
import cv2
import numpy as np
from skimage.feature import local_binary_pattern
import matplotlib.pyplot as plt
# 이미지 읽기
image_path = 'Write your image path'
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
# LBP 계산
radius = 1
n_points = 8 * radius
lbp = local_binary_pattern(image, n_points, radius, method='uniform')
# 결과 시각화
plt.figure(figsize=(8, 8))
plt.subplot(1, 2, 1)
plt.title('Original Image')
plt.imshow(image, cmap='gray')
plt.subplot(1, 2, 2)
plt.title('LBP Image')
plt.imshow(lbp, cmap='gray')
plt.show()
위는 LBP 예제 코드입니다. example.jpg라는 이미지를 읽어 해당 이미지의 LBP matrix(image)를 출력해줍니다.
환경이 갖추어져 있다면, 여러분들이 분석하고자 하는 image의 path만 image_path에 넣어주시면 됩니다.
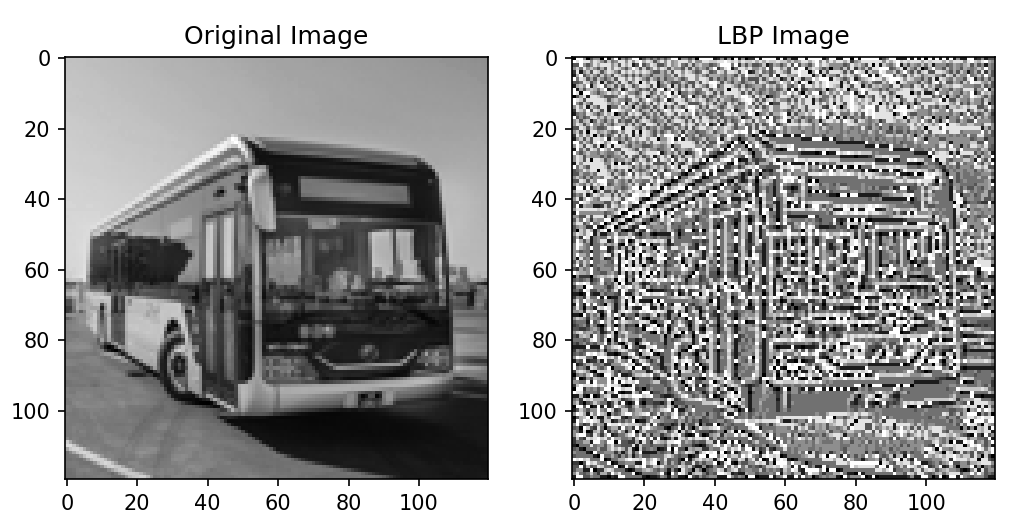
저는 여기에 버스 사진을 넣어보았고, 결과는 아래와 같습니다.
[1] - 2. GLCM (Grey Level Co-occurrence Matrix)
grey 이미지 내에서 특정한 패턴을 이루는 픽셀의 쌍이 일정 거리와 각도에서 얼마나 자주 발생하는지를 행렬로 나타냅니다. 이를 통해 반복되는 패턴에 대한 대비, 상관, 에너지, 동질성 등의 성질을 알 수 있습니다.
여담이지만, 강의를 듣거나 공부를 하다보면 grey와 gray를 항상 혼용했어서 뭐가 맞는 표현인지 헷갈렸었는데, 둘 다 맞다고 합니다. (gray는 미국식, grey는 영국식 표기)
이건 개념이 조금 어렵습니다. 기본적으로 greyscale의 (N x N) Image Matrix가 있고, 이 matrix의 greyscale 값을 L 이라고 합시다. 설정한 co-occurrence Matrix를 P[i,j]라고 합시다. 거리 d = (dx,dy)는 기준 픽셀 (위의 LBP에서 '나'에 해당합니다)로부터 떨어진 거리입니다.
기준 픽셀의 값과 그로부터 d만큼 떨어진 픽셀의 값이 각각 i,j가 됩니다. 그리고, P[i,j]값을 +1 해주면 됩니다. 여기서 생각을 해보면, 당연히 새로이 만들어지는 co-occurrence Matrix는 (L x L) 의 size를 가지게 됩니다.
이해가 잘 안되시죠? 저도 잘 안됩니다. 같이 예시로 살펴보겠습니다.

여기서 Pd(i,j)의 값은 카운트 된 횟수라고 생각하시면 됩니다.
아래는 GLCM의 예제 코드입니다.
import cv2
import numpy as np
import skimage.feature
import matplotlib.pyplot as plt
# 이미지 읽기
image_path = 'Write your image path'
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
# GLCM 계산
glcm = skimage.feature.greycomatrix(image, distances=[1], angles=[0], levels=256, symmetric=True, normed=True)
# GLCM 특징 추출
contrast = skimage.feature.graycoprops(glcm, 'contrast')[0, 0]
correlation = skimage.feature.graycoprops(glcm, 'correlation')[0, 0]
energy = skimage.feature.graycoprops(glcm, 'energy')[0, 0]
homogeneity = skimage.feature.graycoprops(glcm, 'homogeneity')[0, 0]
# 결과 출력
print(f'Contrast: {contrast}')
print(f'Correlation: {correlation}')
print(f'Energy: {energy}')
print(f'Homogeneity: {homogeneity}')
아까 LBP에서 사용했던 버스 이미지를 돌려보았고, 밑은 그 결과입니다.

여기서 각 결과값의 의미에 대한 설명을 드리겠습니다.
- Contrast : 대비, 클 수록 명확한 경계와 큰 grey-level 차이가 있다
- Correlation : 상관성, 클 수록 이미지에 linear한 구조가 있다는 것 (일정한 패턴)
- Energy : 에너지, 값이 클 수록 이미지에 규칙적이고 반복적인 패턴이 있다는 것
- Homogeneity : 동질성, 클 수록 이미지가 균일하고 부드러우며 큰 밝기 변화 X
[1] - 3. Law's energy
앞서 설명드린 2가지 방법은 Color를 이용하여 Texture를 분석하는 방법이었다면, 이건 Edge를 이용합니다.
1x5 Size의 5가지 필터(혹은 마스크)가 존재하는데 이 필터들을 이용해 Imgae와 convolution하는 방법입니다.
5가지 필터는 다음과 같습니다.
- L5 = [1 4 6 4 1] (Level, 이미지의 밝기 분포를 감지하고 텍스쳐의 전반적인 수준 측정)
- E5 = [-1 -2 0 2 1] (Edge, 경계선을 감지하여 텍스쳐의 변화 지점 포착 - 1차 미분)
- S5 = [-1 0 2 0 -1] (Spot, 점 패턴을 강조하여 작은 객체나 점들을 탐지 - 2차 미분)
- R5 = [1 -4 6 -4 1] (Ripple, 주기적인 패턴을 감지하여 regular한 반복 텍스쳐 포착)
- W5 = [-1 2 0 -2 -1] (Wave, 파형 패턴을 감지하여 random한 반복 텍스쳐 포착)
여기서 각 필터들끼리 convolution을 진행합니다. 예시로, L5와 S5를 convolution하여 L5S5 필터를 만들게 되면
이 L5S5 필터는 밝기 분포와 경계선 탐지에 특화되어있을 것이며, 이러한 필터의 조합은 총 25개가 나올 것입니다.
(근데 L5L5 필터는 밝기만 나타내기에 kernel로는 쓰이지 않고, 추후에 정규화 시에는 사용되게 됩니다.)
그리고 이 때의 L5S5와 같은 필터를 Texture Descriptor 라고 볼 수 있습니다.
또한 L5S5 와 S5L5는 각기 다른 필터일 것이기에, 이 둘을 합쳐주면 rotation에 invarient한 필터가 완성될 것이고,
이 때 만들어진 필터는 L5S5R 이라고 합니다.

밑은 Law's Energy 예시 코드입니다.
# Law's texture
import cv2
import numpy as np
import skimage.feature
import matplotlib.pyplot as plt
from scipy import signal as sg
def laws_texture(gray):
(rows, cols) = gray.shape[:2]
smooth_kernel = (1/25)*np.ones((5,5))
gray_smooth = sg.convolve(gray, smooth_kernel,"same")
gray_processed = np.abs(gray - gray_smooth)
filter_vectors = np.array([[ 1, 4, 6, 4, 1], # L5
[-1, -2, 0, 2, 1], # E5
[-1, 0, 2, 0, -1], # S5
[ 1, -4, 6, -4, 1]]) # R5
# 0:L5L5, 1:L5E5, 2:L5S5, 3:L5R5,
# 4:E5L5, 5:E5E5, 6:E5S5, 7:E5R5,
# 8:S5L5, 9:S5E5, 10:S5S5, 11:S5R5,
# 12:R5L5, 13:R5E5, 14:R5S5, 15:R5R5
filters = list()
for i in range(4):
for j in range(4):
filters.append(np.matmul(filter_vectors[i][:].reshape(5,1),
filter_vectors[j][:].reshape(1,5)))
conv_maps = np.zeros((rows, cols,16))
for i in range(len(filters)):
conv_maps[:, :, i] = sg.convolve(gray_processed,
filters[i],'same')
texture_maps = list()
texture_maps.append((conv_maps[:, :, 1]+conv_maps[:, :, 4])//2) # L5E5 / E5L5
texture_maps.append((conv_maps[:, :, 2]+conv_maps[:, :, 8])//2) # L5S5 / S5L5
texture_maps.append((conv_maps[:, :, 3]+conv_maps[:, :, 12])//2) # L5R5 / R5L5
texture_maps.append((conv_maps[:, :, 7]+conv_maps[:, :, 13])//2) # E5R5 / R5E5
texture_maps.append((conv_maps[:, :, 6]+conv_maps[:, :, 9])//2) # E5S5 / S5E5
texture_maps.append((conv_maps[:, :, 11]+conv_maps[:, :, 14])//2) # S5R5 / R5S5
texture_maps.append(conv_maps[:, :, 10]) # S5S5
texture_maps.append(conv_maps[:, :, 5]) # E5E5
texture_maps.append(conv_maps[:, :, 15]) # R5R5
texture_maps.append(conv_maps[:, :, 0]) # L5L5 (use to norm TEM)
TEM = list()
for i in range(9):
TEM.append(np.abs(texture_maps[i]).sum() / np.abs(texture_maps[9]).sum())
return TEM
# 이미지 읽기
image_path = 'Write your image path'
image = cv2.imread(image_path, cv2.IMREAD_GRAYSCALE)
laws = laws_texture(image) # 9-d
print(laws)
아래는 마찬가지로 버스 이미지를 입력 이미지로 주었을 때의 결과입니다.

'컴퓨터비전 (CV)' 카테고리의 다른 글
| [컴퓨터비전] (5) Linear Regression, 선형회귀분석 (5) | 2024.07.24 |
|---|---|
| [컴퓨터비전] (4) Image Segmentation, 이미지 분할 (0) | 2024.07.12 |
| [컴퓨터비전] (3) Shape에 대하여 (0) | 2024.06.14 |
| [컴퓨터비전] (1) Color, Edge에 대하여 (0) | 2024.03.31 |



