[데이터사이언스] 넓고 얉은 데이터사이언스

중간고사 당일 말아주는 막학기 대학생의 벼락치기 START

 

(제정신이 아니라 글에 맥락이 없고 반말입니다 죄송합니다)

 

낭만의 시대는 저물고 이름하야 빅-데이터의 시대가 도래했다

 

오늘은 데이터, 데이터사이언스, 데이터마이닝이란 무엇인지에 대해 넓고 얇게 알아보려한다.

각 사항에 대한 자세한 포스팅은 추후에. 미래의 나 파이팅.

 

 

 

  |  데이터의 유형

 

데이터사이언스의 관점에서 데이터는 사실과 관찰을 기반으로 하는 정보의 집합으로, 다양한 형태로 존재할 수 있다.

 

 

이러한 데이터는 크게 2가지 유형으로 나뉜다.

 

1. Structured data (정형 데이터) : 구조화된 형식을 가지며 행과 열의 형태를 갖춘 DB나 엑셀 시트 같은 데이터.

2. Unstructured data (비정형 데이터) : 정해진 형식이 없는 데이터로 이미지, 텍스트, 오디오, 비디오 등의 다양한 형태를 포함한다.

 

 

 

  |  데이터의 종류

 

다음은 데이터의 종류, Type에 대해 알아보자.

 

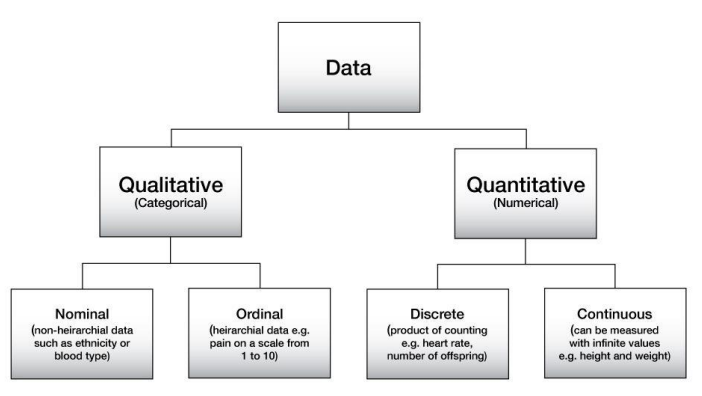
데이터는 크게 Qualitative한 질적 데이터 / Quantitative한 양적 데이터로 구분할 수 있으며, 그 안에서도 하위 분류로 나뉘게 된다.

 

Qualitative한 질적 데이터는 숫자로 표현할 수 없는 데이터라고 이해하면 편하다. 주로 특성을 나타내는데, 그 안에서도 이름이나 레이블로만 구분되며 순서가 없는 Nominal한 명목형 데이터와 순서를 가지고 있는 Ordinal한 서열형 데이터로 나뉘게 된다. 예시로, 어떤 군인의 국적은 Nominal data이며 그 사람의 계급은 Ordinal data에 속한다.

 

Quantitative한 양적 데이터는 숫자로 표현할 수 있는 데이터라고 생각하면 되며, 이 양적 데이터는 하위 분류로 명확한 정수값을 가지는 Discrete한 이산형 데이터와 무한히 세밀한 구간의 측정값을 가지는 Continuous한 연속형 데이터로 다시 나뉜다. 예시로, 어느 학생의 시험 점수는 Discrete data이며 그 학생이 시험을 보는데 걸린 시간은 Contiuous data이다.

 

Quantitative한 Discrete data였던 학생의 시험 점수를 각 급간으로 나누어 A, B, C 등의 학점으로 환산하게 된다면 이는 Qualitative한 Ordinal data가 되듯이 각 데이터의 종류는 그의 분류 및 평가 방식에 따라 변할 수 있다.

 

 

 

  |  데이터 사이언스

 

데이터를 수집, 분석, 해석하는 종합적인 과정으로 데이터마이닝을 포함하여 더 넓은 범위의 활동을 포괄한다. 정형화된 데이터 뿐만 아니라 비정형 데이터인 이미지 /  텍스트 / 음성 데이터 등을 전부 다루며, 더 복잡한 문제를 해결하는 것을 목표로 한다. 

 

 

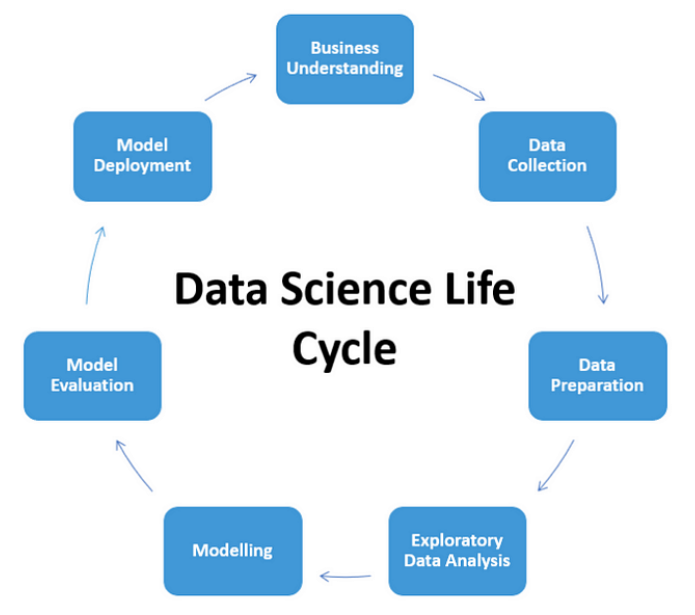
주요 목표로는 데이터를 통해 문제를 해결하거나, 예측 모델을 만들거나, 새로운 지식을 창출하는 것.

 

사용하는 기술들은 휘황찬란하다. 기계학습, 딥러닝, 자연어처리(NLP), 컴퓨터비전(CV) 등등... 내가 열심히 포스팅한 대부분의 글들이 이 데이터사이언스에 속한다고 볼 수 있다. 오늘은 데이터 사이언스의 한 부분집합으로 데이터마이닝을 공부해보겠다.

 

매우 간단한 데이터 사이언스 예시를 NLP 분야에서 찾아보자. 어떤 문서에서 중요한 단어 w 를 찾으려할 때, TF-IDF를 사용할 수 있다. 여기서 TF(w)는 특정 단어 w가 한 문서 내에서 얼마나 자주 등장했는지를 측정한 지표이고, IDF(w)는 특정 단어 w가 등장하는 문서 수와 전체 문서 수의 비율을 측정한 지표이다.

 

이 둘을 곱한 값인 TF-IDF(w)를 통해 우리는 특정 단어가 한 문서 내에서 자주 등장하면서도 전체 문서 집합에서는 드물게 등장할수록 그 단어의 중요도가 높다는 것을 알 수 있다.

 

너무나도 방대한 분야이기에, 더 다양하고 자세한 포스팅은 나중으로 미루겠다.

 

 

 

  |  데이터 마이닝

 

데이터 사이언스에 속하는 하나의 분야로, 대량의 데이터 속에서 유용한 패턴, 규칙, 트렌드를 찾아내고 의미 있는 정보를 추출하는 과정을 말한다. 데이터 마이닝에서는 주로 정형화된 데이터를 다루게 된다.

 

데이터마이닝 vs 데이터사이언스 (feat. ChatGPT)

 

주요 목표로는 패턴 발견, 예측 모델링, 데이터 분류(Classfication), 데이터 군집화(Clustering), 연관 규칙 학습 등이 있다.

사용 분야로는 마케팅, 의료, 금융, SNS 등 다양한 활용 사례가 있다. 대부분의 일상 속에 녹아있는 듯 하다.

 

다양한 Data quality (~=분포유형) 예시

 

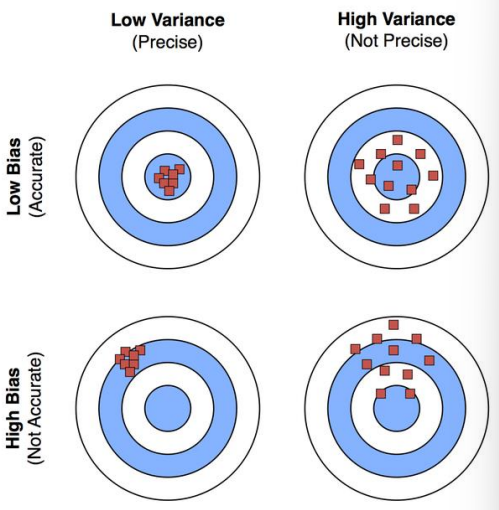
이러한 데이터마이닝을 할 때 몇 가지 고려해야할 점이 있다. 데이터의 원활한 가공 및 처리를 위해 Data type을 정해야 하고, 지나치게 편향되거나 missing 되는 등의 Data quality를 생각해야하며, 데이터 분석 시 연산량 등을 고려하여 Data preprocessing을 해주어야하고, 의미있는 정보를 알아내기 위해 데이터 간 유사도인 Data similarity를 어떻게 측정할지 고려해야한다. 

 

위 과정을 종합하여 데이터마이닝을 하는 주요 기법 중 오늘 알아올 아이들

 

-  1. 회귀 분석 (Regression)

-  2. 결정 트리 (Decision tree)

-  3. 차원 축소 (Dimensionality reduction)

-  4. 인공 신경망 (ANN)

-  5. k-최근접 이웃 알고리즘 (k-NN) 

 

등이 있고, 오늘은 이 기법들에 대해서 알아볼 것이다.

 

 

1. 회귀 분석 (Regression)

 

사실 요건 이미 내가 포스팅 했던 내용도 있다. 크게 다를 건 없으니 Linear regression은 아래 포스팅 참고 바람.

https://dev-easyhun.tistory.com/9

[컴퓨터비전] (5) Linear Regression, 선형회귀분석

 

그러나 위의 포스팅에서는 선형 회귀분석만 다루었었다. 여기서는 Rogistic regression에 대해 알아보려 한다.

 

로지스틱 회귀 (Rogistic regression) 는 주로 이진 분류 문제를 해결하기 위해 사용되는 모델이다.

앞서 배운 선형 회귀가 입력 값을 정량적인 특정 값으로 예측하는 모델이었다면 로지스틱 회귀는 입력값이 어느 클래스에 속할지 예측, 즉 classification 하는 데 중점을 두고 있다. 

 

로지스틱 회귀에서는 로짓(logit)이라는 값을 계산하는데, 로짓 z = β0 + β1*x1 + β2*x2 + ... + βn*xn 라는 선형 방정식을 사용한다. 이러한 로짓 값 z를 로지스틱 함수를 통해 0과 1 사이의 확률로 계산하고, 이 계산된 확률 값을 Thresold 기준으로 나누어 클래스를 결정하게 된다.

 

h(x)는 계산된 확률값 z, 우측 그래프는 로지스틱 함수 (여기서는 sigmoid)

 

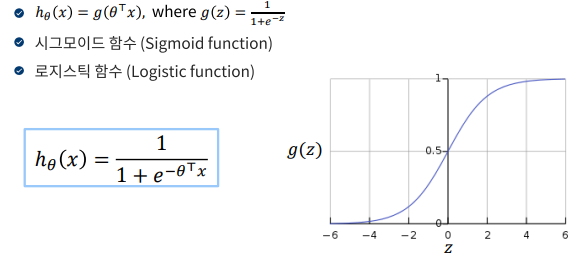
당연하게도 여기서도 비용함수(손실함수)가 발생하게 된다. 

로지스틱 회귀의 비용함수 J

 

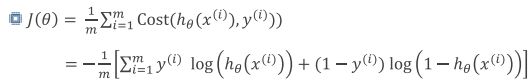
위와 같은 손실 함수를 가지는데, 보기가 어렵다면 아래와 같이 생각하면 편하다.

 

 

모델의 성능을 향상시키기 위해 위의 비용함수 값을 최소로 만들어주는 것이 목표인데, 이 때 주로 사용하는 것이 경사하강법(Gradient descent)이다. 경사하강법은 위의 선형 회귀 분석 포스팅에 잘 작성해두었으니 참고 바람.

 

여담으로, 변수가 여러 개인 다중 회귀 분석 시에 상관계수가 높은 독립변수 쌍이 있다면 회귀 모델의 성능이 저하될 수 있다. ( [ex] y' = 창업비용 / x1 = 위치 / x2 = 월세 인 경우, x1과 x2는 서로 상관계수가 매우 클 것이다. y'을 예측하는 데 변수가 두 번 들어가는 들어가는 꼴이 되어 성능 저하의 가능성이 있음)

 

위와 같은 문제는 다중공선성(Multicollinearity) 때문에 생기게 되는데, 이럴 때는 위의 쌍에서 한 독립변수를 빼거나 후술할 PCA를 통해 차원도 줄이고 성능도 높이고 일석이조할 수 있다.

 

 

 

2. 결정 트리 (Decision tree)

 

나름 가벼운 파트이다. 결정 트리는 질문의 연속이라고 생각하면 좋은데, 일종의 스무고개를 한다고 생각하면 된다.

 

결정 트리 예시

 

Decision tree는 지도 학습 알고리즘 중 하나로, 회귀/분류 문제에 널리 활용된다. 각 노드로 표현된 데이터의 특성을 기반으로 의사 결정을 시각적으로 표현한 구조를 띄며, 쉽게 해석할 수 있다는 장점이 있다.

 

 

 

3. 차원 축소 (Dimensionality reduction)

 

(x,y)로 이루어진 2차원 데이터가 있다.

(x,y,z)로 이루어진 3차원 데이터가 있다.

....

(x,y,z,...,n)로 이루어진 N차원 데이터가 있다.

 

차원이 무작정 크면 좋을까?

정답은 ''아니오''다.

 

차원이 증가할 수록 이를 표현하기 위한 parameter는 증가할 것이고, 그를 표현하기 위한 데이터 세트는 기하급수적으로 늘어날 것이다. 그렇게 되면 모델 학습을 위한 연산량 또한 많아질 것이며, 데이터 간 유사성을 검사하기 위한 거리를 측정하는 비용도 늘어날 것이다.

 

이를 차원의 저주, Cunse of Dimensionality 라고 하는데, 이와 같은 문제를 해결하기 위해서는 차원을 적당량 축소하는 것이 필요하다. 그렇게 다양한 차원 축소 기법이 등장하게 되었는데, 크게 보면 특징 선택과 특징 추출이 있다.

 

[차원 축소] 특징 선택 / 특징 추출 기법들

 

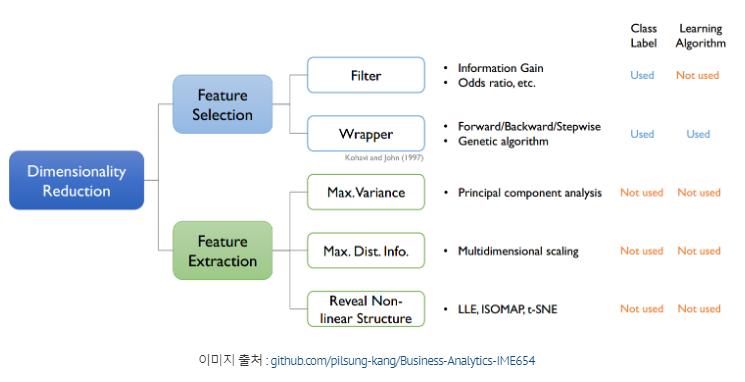
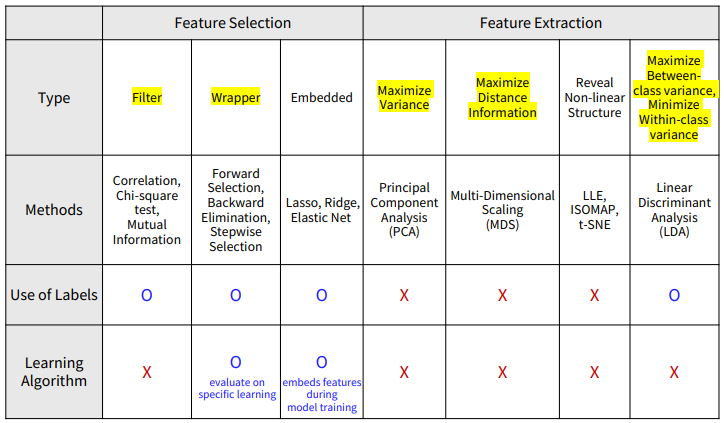
특징 선택(Feature selection)은 기존의 특성 중 가장 중요한 특성만을 선택하여 사용하는 과정이고, Filter / Wrapper / Embedded 방법 등이 있다.

 

특징 추출(Feature extraction)은 원본 데이터를 변형하거나 요약하여 새로운 특성을 생성하는 과정으로 PCA / LDA / Deep auto encoder 등이 있다.

 

특징 선택 / 특징 선택 기법들의 detail 사항

 

이 중 특징 추출 기법 중 하나인 PCA, 주성분 분석을 간단히 설명하자면, 기존의 {x1, x2, ... , xn} 의 특징이 있다고 치자.

위의 특징들을 가중치 합으로 결합한 새로운 특징 Xnew = w1x1 + w2x2 + ... + wnxn 으로 나타내는데, 여기서 각각의 w들을 주성분이라 부른다. 각각의 주성분은 데이터의 분산이 최대화되는 방향을 나타낸다. 이를 통해 데이터의 차원을 줄이면서도 가능한 많은 정보를 유지하는 것이 가능해진다.

 

 

 

4. 인공 신경망 (ANN)

 

인공신경망, Artificial Neural Network 는 인간의 뇌 신경망을 본뜬 알고리즘으로, 데이터마이닝 뿐만 아니라 기계학습 전반에 걸쳐 자주 사용되는 강력한 도구다. ANN은 뉴런(Neuron) 과 계층(Layer) 으로 구성된 계층적 구조를 따르며, 이 계층을 통해 입력 데이터를 전달하고 각 계층에서 연산을 통해 예측을 내린다.

 

구성 요소로는 데이터가 처음 입력되는 계층인 입력층(Input Layer) , 최종 예측값을 출력하는 출력층(Output Layer) , 입력층과 출력층 사이에 위치한 계층인 은닉층(Hidden Layer) , 각 뉴런 간의 연결에 부여되는 가중치(Weights) , 각 뉴런에서 추가적인 학습을 돕는 편향(Bias) 이 있다.

 

단일 퍼셉트론

 

다수의 뉴런을 통해 받은 가중합을 통해 하나의 예측값을 결정하는 알고리즘을 퍼셉트론이라 하는데, 위의 사진 퍼셉트론의 예시이다. ANN은 위와 같은 퍼셉트론들이 모여 서로 연결된 계층적 구조를 띄는 형태를 가지고 있으며, 사진으로 보면 아래와 같다.

 

ANN, 다층 퍼셉트론

 

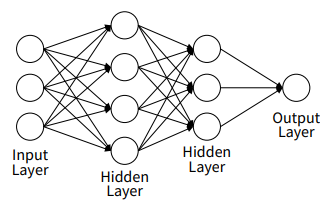
여기서 각 뉴런은 입력 데이터를 받고, 이를 가중치와 결합하여 계산한 뒤 ( z = w1​x1 ​ + w2​x2 ​+ ⋯ + wn​xn​ + b )

활성화 함수를 통해 출력값을 결정한다. ( a=f(z) )

 

 

활성화 함수들

 

대표적인 활성화 함수로는 sigmoid, reLU, Softmax 함수가 있다.

 

 

 

5. k-최근접 이웃 알고리즘 (k-NN) 

 

k-Nearest Neighbors 알고리즘은 지도 학습에서 사용되는 비선형 분류/회귀 알고리즘입니다. 쉽게 말해 새로운 데이터가 들어오면 그와 가장 가까운 거리의 k개의 데이터의 label을 참고하여 예측 및 분류를 합니다. 다른 방법들은 모델 설계 단계에서만 training dataset을 활용한 후 만들어진 모델로 예측 및 분류를 수행한다면, k-NN은 따로 만드는 모델 없이 각각의 예측 시에 training dataset을 활용한다는 것입니다.

 

k-NN classfication 예시, NEW 데이터는 파랑이로 분류된다 (if k=3)

 

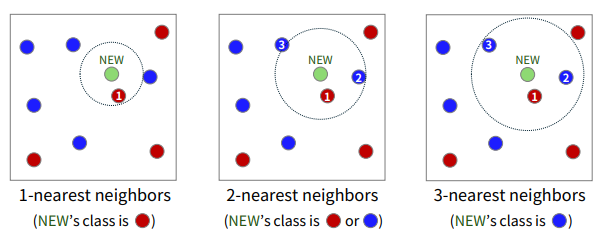
알고리즘은 이렇습니다. 새로운 데이터와 기존 모든 데이터의 거리를 계산합니다. 이후 가장 가까운 k개의 데이터 포인트(이웃)을 선택하고, 분류인 경우 k개 중 가장 많이 나타난 데이터 클래스로 분류합니다. 회귀인 경우 k개 값의 평균 혹은 가중 평균을 계산하여 예측 값을 구합니다.

 

데이터 간 거리 구하기

 

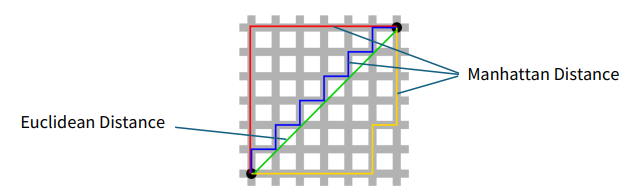
여기서 새로운 데이터와 기존 데이터들간의 거리를 구할 때, 일반적으로는 유클리드 거리를 사용합니다. (초록)

그러나 사진 상의 맨해튼 거리(빨강=파랑=노랑), cosine similarity 등을 사용할 수도 있습니다.

 

k-NN 같은 경우 간단하고 직관적이며 훈련 단계에서 모델의 학습이 없다는 장점이 있지만, 각 예측 마다 계산 비용이 O(n)으로 큰 점과 k값에 민감하다는 단점이 있습니다.

 

정신이 없어서 여기는 존댓말로 작성했군요. 조금 더 겸손해진 느낌입니다.

 

 

 

  |  Pandas & Numpy in Python

 

앞서 공부한 데이터 분석 기법들을 사용하기 위해 주로 사용되는 Python 라이브러리들이다.

 

Pandas는 데이터 조작 및 분석을 위한 라이브러리로 Data Frame(df)라는 자료구조를 주로 사용하고, Numpy(np)는 수치 계산을 위한 라이브러리로 다양한 수학 함수 및 최적화된 연산을 지원한다.

 

데이터를 불러와 마스킹하여 관계를 시각화를 하는 간단한 코드를 작성해보면 다음과 같다. 시각화를 위해 널리 사용되는 matplotlib.pyplot , seaborn 등의 라이브러리를 추가로 사용하였으며, 데이터 파일은 sklearn을 통해 불러오면 되겠다.

 

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 1. 데이터 로드
housing_df = pd.read_csv('BostonHousing.csv')

# 2. 데이터의 기초 통계량 확인
print("기초 통계량:\n", housing_df.describe())

# 3. 결측치 확인
print("\n결측치 수:\n", housing_df.isnull().sum())

# 4. 결측치 제거
housing_df = housing_df.dropna()

# 5. 평균값 계산
mean_medv = housing_df['MEDV'].mean()
print(f"\n주택 가격 중위수(MEDV)의 평균값: {mean_medv:.2f}")

# 6. 평균값 이상인 데이터 마스킹
above_average_df = housing_df[housing_df['MEDV'] > mean_medv]

# 7. 평균값 이상인 데이터 확인
print("\n주택 가격 중위수(MEDV)가 평균값 이상인 데이터:\n", above_average_df)

# 8. RM (주택당 방 수)와 MEDV (주택 가격 중위수) 간의 관계 시각화
plt.figure(figsize=(10, 6))
sns.scatterplot(x='RM', y='MEDV', data=housing_df, label='전체 데이터', alpha=0.5)
sns.scatterplot(x='RM', y='MEDV', data=above_average_df, color='red', label='MEDV > 평균값', alpha=0.8)
plt.title('주택당 방 수(RM)와 주택 가격 중위수(MEDV) 간의 관계')
plt.xlabel('주택당 방 수 (RM)')
plt.ylabel('주택 가격 중위수 (MEDV)')
plt.axhline(mean_medv, color='orange', linestyle='--', label='MEDV 평균값')
plt.legend()
plt.grid()
plt.show()

# 9. RM의 평균값 계산 및 출력
mean_rm = np.mean(housing_df['RM'])
print(f"\n주택당 방 수(RM)의 평균값: {mean_rm:.2f}")

# 10. RM의 분포 시각화
plt.figure(figsize=(10, 6))
sns.histplot(housing_df['RM'], bins=30, kde=True)
plt.title('주택당 방 수(RM)의 분포')
plt.xlabel('주택당 방 수 (RM)')
plt.ylabel('빈도수')
plt.grid()
plt.show()